Check Pagerank

Google Pagerank Computation

PageRank can be computed either iteratively or algebraically. The iterative method can be viewed as the power iteration method or the power method. The basic mathematical operations performed are identical.

Iterative

At $t=0$ , an initial probability distribution is assumed, usually

$PR(p_i; 0) = \frac{1}{N}$ .

At each time step, the computation, as detailed above, yields

$PR(p_i;t+1) = \frac{1-d}{N} + d \sum_{p_j \in M(p_i)} \frac{PR (p_j; t)}{L(p_j)}$ ,

or in matrix notation

$\mathbf{R}(t+1) = d \mathcal{M}\mathbf{R}(t) + \frac{1-d}{N} \mathbf{1}$ , (*)

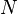where $\mathbf{R}_i(t)=PR(p_i; t)$ and $\mathbf{1}$ is the column vector of length $N$ containing only ones.
The matrix 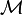$\mathcal{M}$ is defined as

$\mathcal{M}_{ij} = \begin{cases} 1 /L(p_j) , & \mbox{if }j\mbox{ links to }i\ \\ 0, & \mbox{otherwise} \end{cases}$

i.e.,

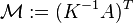$\mathcal{M} := (K^{-1} A)^T$ ,

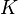where $A$ denotes the adjacency matrix of the graph and $K$ is the diagonal matrix with the outdegrees in the diagonal.
The computation ends when for some small $\epsilon$

$|\mathbf{R}(t+1) - \mathbf{R}(t)| < \epsilon$ ,

i.e., when convergence is assumed.

Algebraic

For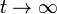 $t \to \infty$ (i.e., in the steady state), the above equation (*) reads

$\mathbf{R} = d \mathcal{M}\mathbf{R} + \frac{1-d}{N} \mathbf{1}$ . (**)

The solution is given by

$\mathbf{R} = (\mathbf{I}-d \mathcal{M})^{-1} \frac{1-d}{N} \mathbf{1}$ ,

with the identity matrix $\mathbf{I}$ .
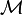The solution exists and is unique for $0 < d < 1$ . This can be seen by noting that $\mathcal{M}$ is by construction a stochastic matrix and hence has an eigenvalue equal to one as a consequence of the Perron–Frobenius theorem.

Check Pagerank Page rank Google page rank check page rank check google pagerank pagerank check google pagerank checker check pagerank Check page rank google

Senin, 05 November 2012

Google Pagerank Computation

Google Pagerank Computation

Iterative

Algebraic